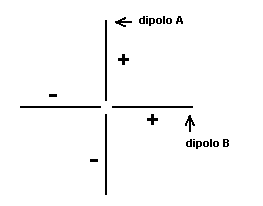POLARIZAÇÃO DE ONDAS

Atualizada em 22/11/2011

Por PY4ZBZ

Figuras animadas de András Szilágyi e Takuichi Hirano ©

Link original : http://www.qsl.net/py4zbz/antenas/polarizacao.htm

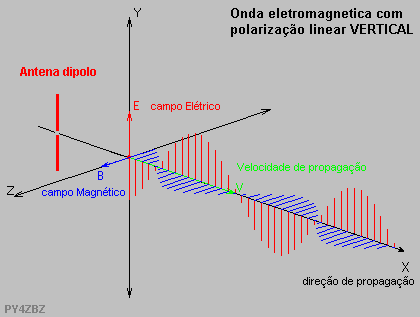
Toda onda eletromagnética é composta de dois campos, o elétrico e o magnético, sempre situados em planos ortogonais (planos fisicamente a 90 graus), e variando em fase (0 graus). Estes campos se propagam em qualquer material isolante (dielétrico) com uma velocidade de propagação, cujo vetor está a 90 graus dos vetores campo elétrico e magnético. No vácuo, esta velocidade é a da luz.

Um dipolo posicionado verticalmente, alimentado por um gerador de freqüência F, gera portanto uma onda eletromagnética polarizada verticalmente, pois o componente campo elétrico está no plano vertical (e conseqüentemente, o componente campo magnético está no plano horizontal). Veja a figura seguinte, onde aparecem os três vetores E, B e V, com 90 graus físicos entre qualquer um deles, com E e B variando em fase ou com zero graus de defasamento elétrico, característica básica da onda eletromagnética:

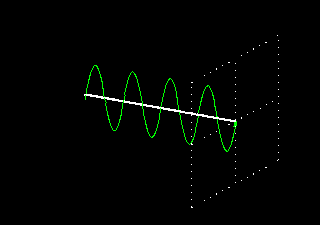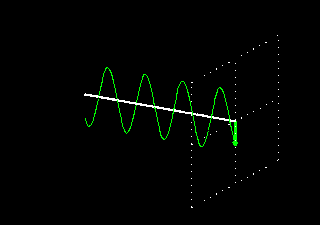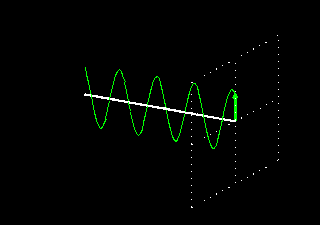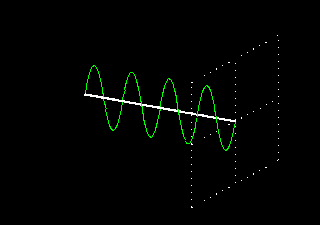
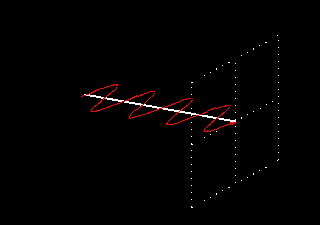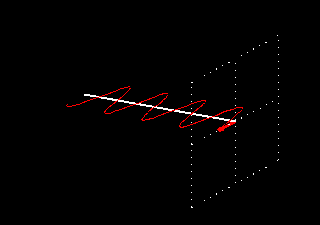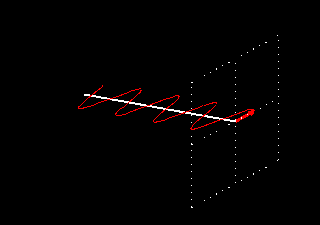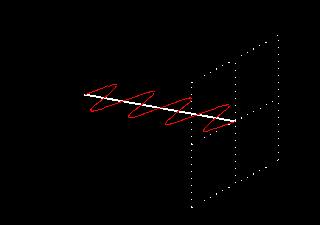
Como esta onda está sempre situada no mesmo plano, é chamada de onda com polarização linear.

As figuras animadas seguintes ilustram uma onda com polarização linear vertical, mostrando apenas o vetor do campo elétrico (o magnético está sempre presente e a 90 graus físicos):

As figuras animadas seguintes ilustram uma onda com polarização linear horizontal, mostrando apenas o vetor do campo elétrico (o magnético está sempre presente e a 90 graus físicos):

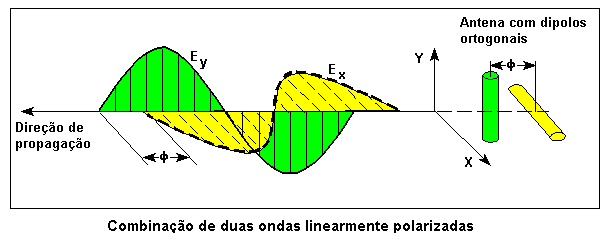
A combinação de duas ondas linearmente polarizadas, uma vertical e outra horizontal, e eletricamente em fase, resulta em uma onda linearmente polarizada inclinada, como pode ser visto nas figuras animadas seguintes:

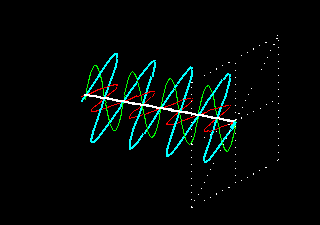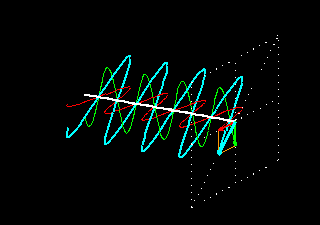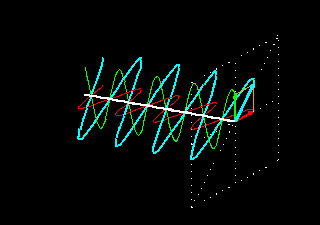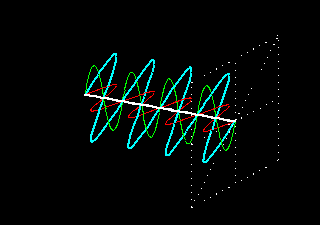
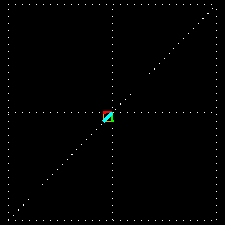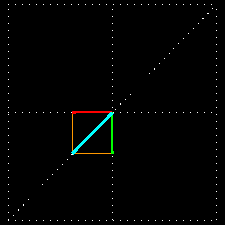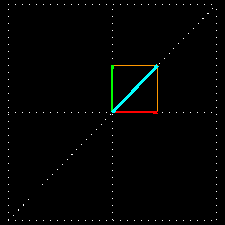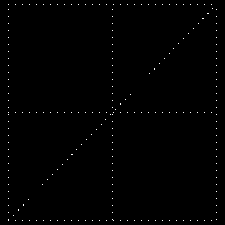
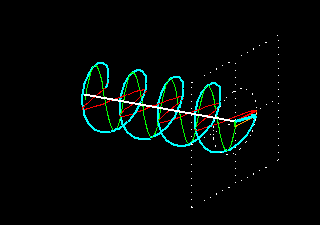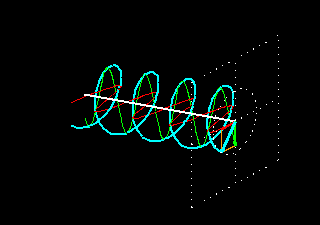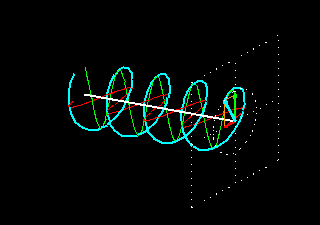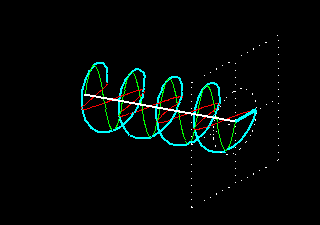
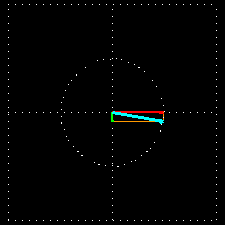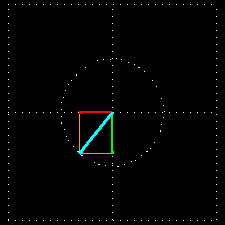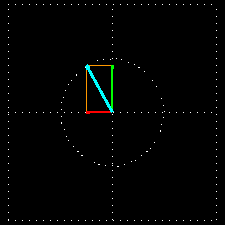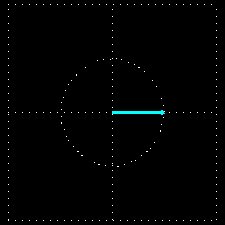
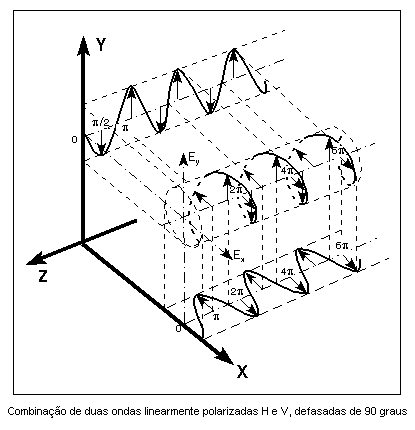
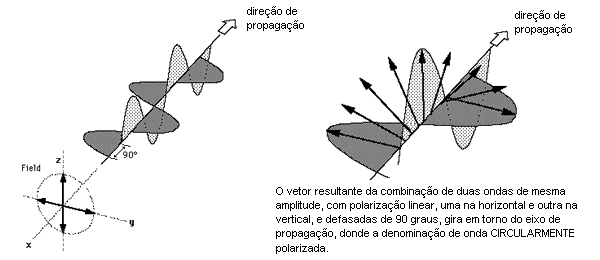
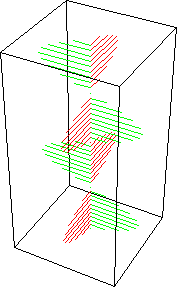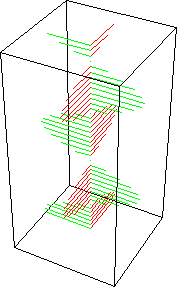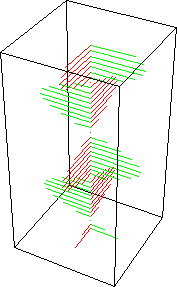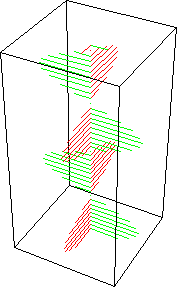
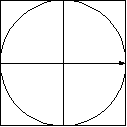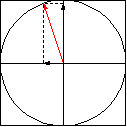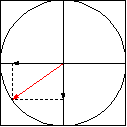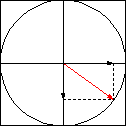
A combinação de duas ondas linearmente polarizadas, uma vertical e outra horizontal, de mesma amplitude e eletricamente defasadas de 90 graus, resulta em uma onda circularmente polarizada, (da mesma forma que uma figura de Lissajous) como pode ser visto nas figuras animadas seguintes:

As figuras seguintes mostram também como é obtida uma onda de polarização circular:

O exemplo acima é de uma onda LHCP , veja definição IEEE a seguir:

Definição de RHCP e LHCP (norma da IEEE)

A figura seguinte mostra dois dipolos cruzados A e B, sendo B alimentado com 90 graus de defasamento (atrasado) em relação ao dipolo A, e alimentados com as polaridades instantâneas indicadas (+). No pico positivo da tensão senoidal aplicada ao dipolo A, este gera o vetor 1, que será o primeiro a deixar a antena e a atravessar o plano. Um quarto de período mais tarde, é a vez do dipolo B receber o pico positivo da senóide, pois está atrasado 90 graus, e gerar então o vetor 2, que será o segundo a atravessar o plano imaginário, e assim por diante, quando chegar o pico negativo no dipolo A gerando o vetor 3, e depois o pico negativo da senóide no dipolo B gerando o vetor 4 :

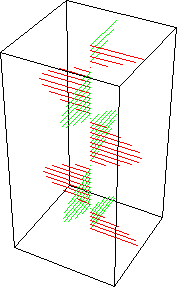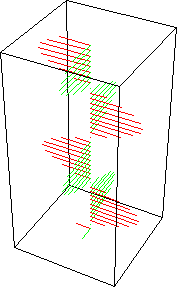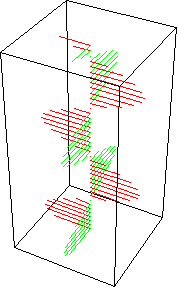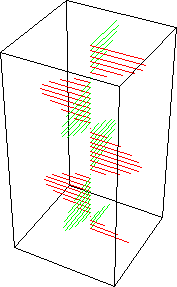
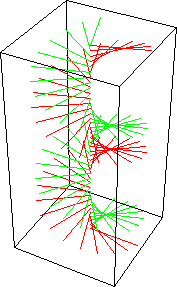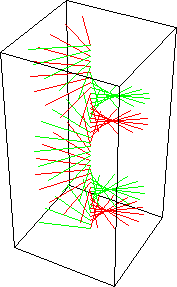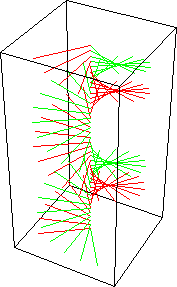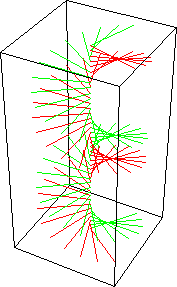
Na figura anterior, temos uma onda com polarização circular à direita (em inglês: RHCP Right-Hand Circular Polarization), porque o vetor gira no sentido anti-horário (regra da mão direita) ao atravessar um plano imaginário e perpendicular ao eixo de propagação, e visto pelo lado do plano por onde a onda sai deste plano (os planos quadrados nas figuras animadas anteriores). Evidentemente, visto pelo lado por onde a mesma onda entra no plano, a rotação fica invertida: no sentido horário ! como acontece quando se olha na direção de propagação por trás da fonte (IEEE).

ATENÇÃO: Por isso há bastante confusão sobre o assunto... e também porque em óptica clássica, a definição para luz com polarização circular é invertida em relação a definição da IEEE para antenas e ondas de radio, que é adotada pela AMSAT, e outras entidades. A luz do sol por exemplo, é polarizada randomicamente em todos os planos, por isso é chamada de não polarizada, pois não é nem linear e nem circular. Filtros ópticos polarizadores permitem separar determinados planos de polarização da luz natural.

 Trocando a fase para +90 graus, ou invertendo a polaridade (fase) de uma das ondas, teremos uma onda com polarização circular a esquerda LHCP (Left-Hand circular polarization). O vetor campo elétrico (e magnético também !) de uma onda circularmente polarizada, gira com uma velocidade de rotação igual a freqüência da onda, pois faz uma volta completa por ciclo !. Apenas para entender melhor, poderíamos obter uma onda circularmente polarizada, girando um dipolo com uma velocidade igual a freqüência do sinal...ou seja, em 100 MHz, girando o dipolo 100.000.000 de vezes por segundo !

Vermelho: campo elétrico, verde: campo magnético.  Direção de propagação: de baixo para cima.

a	b	a+b      (vista saindo do plano)
abs(a)=1, arg(a)=0°	abs(b)=1, arg(b)=-90°	RHCP

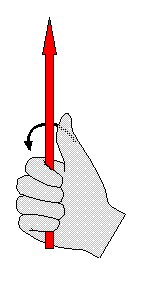
a e b : as duas ondas linearmente polarizadas e defasadas 90 graus; a+b : a onda RHCP resultante.

O nome RH e LH (Right-Hand, mão direita e Left-Hand, mão esquerda) é derivado da analogia seguinte:

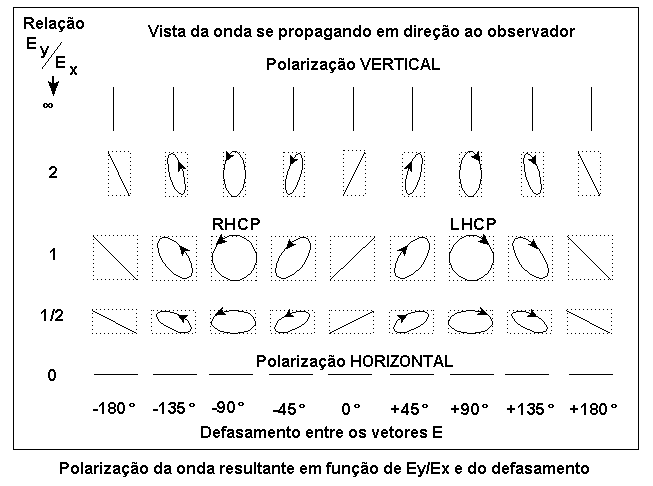
Se a rotação for contraria a da figura acima, aplica-se a regra da mão direita: RHCP.

A figura seguinte mostra o resultado da combinação de duas ondas linearmente polarizadas e ortogonais, com diferentes relações de amplitudes e defasamentos, mostrando que a resultante pode ser polarização linear V / H / inclinada, elíptica ou circular. Detalhe importante: nesta figura a onda é vista se aproximando do observador (ou saindo do plano), portanto a onda RHCP agora roda no sentido anti-horário ! Cuidado, tudo é relativo:

A figura seguinte mostra a analogia entre onda circularmente polarizada RHCP e parafusos com rosca à direita, e mostra porque as duas antenas TX e RX de um enlace devem ter polarizações idênticas, ou co-polarizadas (veja a nota na definição IEEE acima):

Para quem gosta de matemática, observe a posição do Pi/2 (=90 graus), que tanto pode afetar a fase de alimentação (Omega t) como o deslocamento axial (k z), donde os dois métodos explicados mais adiante:

Vantagens da polarização circular:

Uma vantagem da polarização circular é não ser afetada pela rotação de Faraday em ondas que atravessam a atmosfera e ou a ionosfera, principalmente em comunicações via satélite. Outra vantagem é que não é necessário ajustar a polarização das antenas (posição em torno do eixo de propagação) como acontece com antenas linearmente polarizadas.

Características da polarização circular:

Uma característica da polarização circular é que muda o sentido de rotação quando refletida por um plano condutor, como por exemplo, refletores planos ou parabólicos, reflexão lunar, etc... Na onda linearmente polarizada, muda somente a fase (inversão ou 180 graus), quando refletida. Outra característica da polarização circular é a razão axial, que é a relação das amplitudes dos vetores no plano X pelo plano Y. Num circulo perfeito, esta relação é 1, ou 0 dB. Relação axial diferente de 0 dB significa que a polarização não é perfeitamente circular, mas elíptica.

Antenas circularmente polarizadas.

Método 1 - Do exposto acima, pode se deduzir que para obter antenas com polarização circular, a partir de antenas linearmente polarizadas (dipolos ou Yagis, etc..), basta colocar duas destas antenas cruzadas a 90 graus, sem deslocamento longitudinal, e alimentadas com 90 graus de defasamento elétrico (com um cabo com um quarto de onda a mais no seu comprimento em uma das antenas por exemplo):

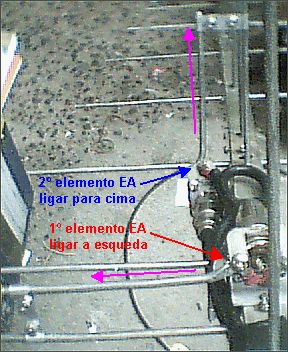
 Método 2 - Outra forma de obter este defasamento é alimentar os dois dipolos em fase, porém deslocando um dos dipolos de um quarto de onda do outro, longitudinalmente no sentido da propagação, como na foto abaixo: 

Obs.: os dois métodos anteriores só geram uma onda com polarização circular  na direção de maior ganho, perpendicular ao plano dos dipolos. Fora desta direção, a onda é elíptica, e a 90 graus desta direção, a onda é linearmente polarizada.

Método 3 - Uma outra forma é usar antenas que já produzem diretamente a polarização circular, como por exemplo as antenas helicoidais (longitudinais ou axiais). De acordo com a IEEE, o sentido de rotação da onda circular gerada por uma helicoidal é o mesmo da rosca de um parafuso gigante na qual a helicóide se encaixaria. Na foto é RHCP, pois tem "rosca" idêntica a de um parafuso com rosca direita:

Importante: antenas como a loop circular, Yagi com aros circulares, magnetic loop, cúbica de quadro, delta loop, etc..., geram todas ondas linearmente polarizadas ! Somente uma helicoidal no modo axial ou longitudinal, ou a correta associação de duas antenas lineares quaisquer, permite obter polarização circular. E duas helicoidais, uma RHCP e a outra LHCP, alimentadas em fase e posicionadas lado lado e no mesmo sentido, geram uma onda com polarização linear !.

Rejeição da polarização cruzada "X-pol rejection" ou "XPD"

Uma característica de qualquer antena (além de ganho, relação frente/costas, impedância, banda passante, etc...), é a sua capacidade (ou não) de rejeição da polarização cruzada "X-pol ou cross-pol rejection ou discrimination XPD"  em dB. Ou seja, é a capacidade da antena em rejeitar a polarização ortogonal a sua, como por exemplo, uma antena com polarização vertical rejeitar a polarização horizontal (e vice e versa) ou uma antena com RHCP rejeitar a LHCP (ou vice e versa). Uma antena perfeita teria rejeição X-pol infinita.

Esta rejeição geralmente só é alta em freqüências de VHF para cima, principalmente em micro-ondas. Rejeição alta de X-pol (20 dB ou mais) permite usar a mesma freqüência para duas transmissões simultâneas e diferentes, uma com RHCP e outra com LHCP, ou uma na vertical e outra na horizontal, como é o caso em satélites de comunicação e TV geoestacionários. Mas as duas antenas (TX e RX) de cada enlace devem ter evidentemente o mesmo tipo de polarização e alta rejeição X-pol. 

Captar uma onda polarizada circularmente com uma antena de polarização linear (ou vice e versa) causa sempre uma perda de 3 dB ! (nem mais, nem menos. Não há rejeição X-pol entre polarizações linear e circular, ou melhor, a rejeição é igual à aceitação: -3dB, pois a onda circular é composta de duas componentes lineares. A antena linear capta apenas uma destas componentes, portanto metade da potencia=-3dB). E captar uma onda RHCP com uma antena LHCP sofre uma perda igual a rejeição de polarização cruzada, que idealmente seria infinita.

Em freqüências abaixo de VHF, como em ondas curtas e medias, a polarização da onda não mantém o seu plano original devido a fenômenos de propagação, e as próprias antenas tem baixa rejeição de X-pol, permitindo assim usar polarizações diferentes na transmissão e recepção, sem muita perda, ou seja, usar indiscriminadamente antenas verticais e horizontais para TX e RX, sem muito prejuízo.

Como obter RHCP ou LHCP com dipolos cruzados.

Mostrarei a seguir como obter na pratica as formas 1 e 2 mencionadas anteriormente. É claro que além de dipolos cruzados, podem ser cruzadas as mais diversas antenas com polarização linear, como Yagis e outras. Mas sempre teremos apenas dois pontos de alimentação, um em cada elemento radiador, denominados dipolos no texto seguinte.

Método 1 :

Os dois dipolos estão na mesma posição longitudinal (no mesmo plano). Portanto devem ser alimentados com um defasamento relativo de 90 graus. A figura seguinte mostra os dipolos vistos por trás, portanto olhando na direção da propagação (se forem de duas Yagis, são vistos pelo lado dos refletores). As polaridades instantâneas indicadas correspondem por exemplo ao condutor interno do coaxial = +, sendo o - a blindagem do coaxial ou o outro lado do balun. Alimentando o dipolo B com um sinal atrazado 90 graus em relação ao dipolo A,  teremos RHCP, pois quando o dipolo A receber o pico positivo da senóide, o B não recebe nada. Quando o B receber o pico positivo, após 1/4 de período, o A não recebe nada. Visto por traz, na direção de propagação, o vetor campo elétrico passa da posição vertical e para cima, para a posição horizontal e para a direita, portanto, rodou à direita ou sentido horário. ao entrar num plano imaginário situado na frente da antena. Invertendo este defasamento relativo ou invertendo a polaridade de alimentação de um dos dipolos, teremos LHCP.

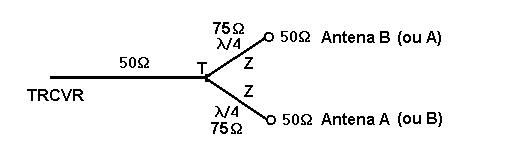
A figura seguinte mostra um exemplo da configuração dos cabos, para antenas com 50 ohms de impedância e obter RHCP, respeitando as polaridades da figura anterior. O trecho de cabo D de 50 ohms e de 1/4 de onda é o que gera o atraso (ou defasamento) relativo de 90 graus, e sem transformar a impedância da antena. Os dois trechos de cabos Z de 75 ohms atuam como transformador de impedância, transformando os 50 ohms de cada antena em 112 ohms, que ligados em paralelo no T, voltam para 50 ohms (na verdade 56 ohms...), e introduzem ambos 90 graus de atraso. Mas o que importa é que a fase da antena B esteja 90 para trás da antena A, o que é feito pelo cabo D.

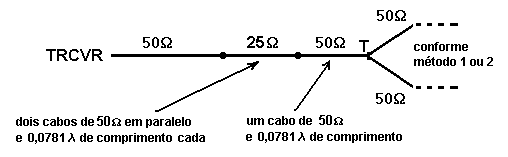
É evidente que os cabos Z também (e somente eles) podem ter comprimentos iguais a múltiplos impares inteiros de 1/4 de onda, o que as vezes facilita a sua instalação, mas desde que os dois cabos também tenham comprimentos iguais. Nunca é demais lembrar que o comprimento de um cabo coaxial é igual ao comprimento elétrico de onda desejado no ar, multiplicado pelo fator de velocidade do cabo. É obvio que também podem ser feitas outras combinações de cabos, desde que se consiga transformar a impedância das duas antenas em paralelo para 50 ohms e ao mesmo tempo os 90 graus de atraso relativo. Trocando a polaridade das conexões de uma das antenas, ou inserindo mais um cabo de meia onda em uma delas, teremos LHCP. Uma outra forma alternativa de ligar os cabos é fazer o paralelo das duas antenas de 50 ohms, o que resulta em 25 ohms no T, e depois transformar estes 25 ohms para 50 ohms, com um cabo de 1/4 de onda e 35 ohms, que pode ser feito com dois cabos de 75 ohms em paralelo, como mostra a figura seguinte:

Método 2 :

Agora os dois dipolos (ou as duas Yagis) são deslocados longitudinalmente de 1/4 de onda (no ar). Portanto as duas antenas agora devem ser alimentadas em fase. Usando novamente a figura dos dipolos anterior, e supondo que o dipolo B está mais perto do observador situado atrás da antena (ou seja, está mais recuado em relação ao A na direção de propagação) teremos RHCP.  A pequena desvantagem deste método é que o boom da antena fica 1/4 de onda mais comprido em relação ao método 1, mas a grande vantagem em relação ao método 1 é que não precisa do cabo defasador D, que pelo fato de ter 1/4 de onda, pode causar transformação indesejável de impedância caso a antena não tenha a mesma impedância que esta cabo !. A figura seguinte mostra um exemplo de interligação:

Continuam valendo as observações anteriores em relação aos cabos Z, e mudança de polarização. Veja um exemplo OZ2OE. Veja mais um exemplo deste método, por PY2BBS. Também pode ser usada a seguinte configuração alternativa de cabos:

E nos dois métodos alternativos anteriores, a transformação de 25 para 50 ohms pode ser ainda mais bem feita usando o transformador de Regier ou 1/12 lambda, como mostra a figura seguinte (não esquecer o fator de velocidade do cabo!), com a grande vantagem de usar somente cabos de 50 ohms !:

(No caso das linhas com 75 ohms, a resultante é 75x75/50=56,25 ohms ou (75/2)x(75/2)/25=56,25 ohms. O transformador acima fornece exatamente 50 ohms a partir de 25 ohms.)

IMPORTANTE: em ambos os métodos 1 e 2, o ganho total das duas antenas continua igual ao ganho de uma só, contrariamente ao que acontece em sistemas colineares, onde as antenas são alimentadas em fase. Se por exemplo, uma antena tem 10 dBi de ganho, duas delas cruzadas e eletricamente a 90 graus pelo método 1 ou 2, terão um ganho total de 10 dBic, o c indicando apenas a polarização circular.

Método intermediário ao 1 e 2 ...

Podemos combinar os dois métodos anteriores (mas para que complicar ?) fazendo com que os 90 graus necessários sejam feitos em parte eletricamente e em parte fisicamente. Por exemplo, podemos deslocar longitudinalmente as duas antenas de 1/8 de onda (no ar) o que equivale a 45 graus elétricos. Ainda faltam 45 graus que serão feitos com um pedaço de cabo de 1/8 do onda a mais em uma das antenas, desde que na antena certa !. Para obter RHCP por exemplo, usamos o exemplo do método 1, mas com o cabo D de 1/8 de onda (não esquecer o fator de velocidade do cabo) e deslocamos as antenas como no exemplo 2, mas apenas de 1/8 de onda no ar. Qualquer outra combinação, como 1/12 de cabo + 1/6 de onda de deslocamento (30 graus +60 graus) também funciona... Uma desvantagem deste método é que não permite inverter de RHCP para LHCP simplesmente trocando a polaridade de uma das antenas.

Conclusão: é evidente que podem ser feitas inúmeras outras formas de interligação, polaridades, comprimentos, deslocamentos, impedâncias de antenas, impedâncias de cabos, etc.. Basta verificar a correta transformação e combinação de impedâncias, e como o vetor onda eletromagnética de cada radiador se situa na direção de propagação em relação ao do outro radiador, incluindo o defasamento elétrico relativo dos dois radiadores:

Trocando em miúdos, veja este exemplo do método 2:

 Na foto acima, temos uma antena feita por Luciano PY2BBS. Ela é vista por trás (como manda a IEEE). O vetor que sai primeiro desta antena é logicamente o do dipolo mais adiantado (mais na frente da antena), que no caso é o dipolo vertical . Como as duas antenas estão alimentadas em fase, na mesma hora que o dipolo vertical recebe o pico positivo da onda senoidal de tensão, gerando um vetor vertical para cima (12 horas no relógio, seta para cima),  o dipolo horizontal também recebe este mesmo pico positivo, e portanto gera um vetor na horizontal e para esquerda (9 horas no relógio). Isto porque a polaridade de ligação dos coaxiais é: condutor interno para cima no dipolo vertical e condutor interno para a esquerda do dipolo horizontal. Como o primeiro vetor a sair da frente da antena é o vertical para cima (12 horas), seguido (apos um tempo de um quarto de período da onda) pelo horizontal à esquerda (9 horas), o vetor, ao se propagar na direção de propagação e olhando por trás, rodou no sentido anti-horário (de 12 para 9 horas), portanto corresponde a uma onda LHCP. Não importa se rodarmos a antena em torno do boom, sempre teremos LHCP, mesmo virando-a de costas. A rosca de um parafuso não muda com a sua posição ! .

  Trocando a polaridade de apenas um dos cabos, por exemplo, ligando o condutor interno do coaxial à direita do dipolo horizontal, teremos RHCP, pois o dipolo horizontal gera agora um vetor horizontal a direita (3 horas) ao mesmo tempo que o dipolo vertical continua gerando o mesmo "12 horas". O primeiro vetor a deixar a antena continua sendo o "12 horas", seguido, um quarto de período depois, pelo "3 horas", portanto girando agora no sentido horário e gerando, de acordo com a IEEE, RHCP. Mas se olharmos de frente para antena, a onda indo em nossa direção (não mais se afastando), o sentido de rotação do vetor é invertido (saindo do plano), mas a polarização é sempre a mesma. Num parafuso com rosca direita, você gira a porca a direita para apertar, e a gira a esquerda para desapertar, mas a rosca sempre é direita.

Detalhe interessante: os dois dipolos também irradiam para trás, em direção ao observador da foto anterior, mas gerando uma onda RHCP !. Esta onda será redirecionada para a frente da antena pelos refletores. Como a onda circular muda de sentido ao ser refletida, esta onda refletida está agora no mesmo sentido LHCP da onda gerada para frente, e portanto se somando construtivamente e contribuindo para o ganho da antena, desde que a distancia relativa refletores/dipolos esteja correta. 

Mais alguns links:

http://www.jawoollam.com/tutorial_polarization.html

http://users.telenet.be/educypedia/electronics/javarf.htm

http://www.g6lvb.com/el/EntryLevelAO-2.htm ou http://www.g6lvb.com/el/Entry%20Level%20AO.pdf

http://www.w1ghz.org/antbook/conf/Helical_feed_antennas.pdf

Satellite_Comms_Polarization.pdf

http://sv1bsx.50webs.com/antenna-pol/polarization.html

http://www.pa3guo.com/dk7zb.html

http://www.pa3guo.com/polarizer.html

 
O meu programa RZ3 permite, entre muitas outras coisas, calcular a inclinação de polarização linear para satélites geoestacionários, em função da posição da antena receptora e do satélite.

Bibliografia:

The satellite experimenter´s handbook.      by Martin Davidoff       ARRL