Cálculo de uma Parábola
para ANTENAS FOCAL POINT, FOCAL FEED po PRIME FOCUS

Atualizada em 03/11/2011

Arquivos reproduzidos com alterações dos originais do mestre Geraldo Paiva no seu site BandaKu

Link Original

Parábolas e Parabólicas

Para se construir uma antena parabólica ou uma antena de moldagem esférica é necessário que alguns conceitos geométricos sejam recordados. É o que buscaremos fazer agora.


1.PARABÓLICA, PARABOLÓIDE, ESFÉRICA, ESFERÓIDE, SIMÉTRICA, ASSIMÉTRICA

Muitos têm sido os técnicos instaladores de antenas, os robistas, os interessados em TV satélite FTA, que navegam em meio a uma série de dúvidas com respeito às antenas mais comumente conhecidas para recepção de TV satélite e genericamente chamadas de parabólicas.

Diante de muitas dúvidas suscitadas nos meios robistas, sobretudo da parte daqueles que iniciam a sua exploração sobre a recepção de sinais de TV Satélite, este sítio de Internet, dentro de sua linha de promover a disponibilização de material educativo, decidiu por elaborar este artigo técnico, objetivando clarear alumas eventuais dúvidas que ainda pairam no meio daqueles que fazem parte de grupos de discussão.

Nós não vamos enfocar a transmissão e recepção profissionais, mas tão somente a recepção doméstica e, desta forma, a linguagem utilizada será sempre aquela que possa ser entendida nessa aplicação e com as características técnicas que essa aplicação possa exigir. Além disso, a despeito de este sítio ser voltado para banda ku, vamos centrar nosso material, com seus exemplos, nas antenas maiores, destinadas à banda C.

Uma antena é dita parabólica por ter a sua forma construtiva derivada de um parabolóide de revolução gerado a partir de uma curva que foi traçada por uma função parabólica. Sua caraterística é que possui um único ponto para onde convergem os sinais refletidos pela sua superfície e só aproveita eficientemente os sinais cuja frente de onda a atinge paralelamente ao seu eixo..

Uma antena é dita esférica por ter a sua forma construtiva derivada de um esferóide de revolução gerado a partir de uma curva que foi traçada por uma função esférica. Sua caraterística é que possui múltiplos pontos para onde convergem os sinais refletidos pela sua superfície e aproveita, por sua vez, todos os sinais cuja frente de onda a atinge proveniente de múltiplas direções. Para um leigo, não faz diferença se a antena é parabólica ou esférica. Seguramente ele atribuirá a ela sempre o nome de parabólica, porque não é fácil distinguir, quando muito se assemelham.

As antenas parabólicas (as parabólicas verdadeiras e as esféricas) são denominadas simétricas se a sua conformação construtiva segue 360 graus do parabolóide ou do esferóide de revolução. No entanto, a antena esférica, mesmo simétrica quanto à superfície do esferóide de 360 graus, terá assimetria quanto aos seus focos, individualmente observados. Uma antena parabólica ou esférica assimétrica propriamente dita é aquela que aproveita apenas parte do parabolóide ou do esferóide de revolução, na sua construção. Essas parcelas de parabolóides ou de esferóides podem ser circulares ovais, quadradas, retangulares, ou podem ter outra modelagem que se queira.

Colocadas essas considerações iniciais, situada a antena parabólica simétrica na variedade de antena existente, vamos nos ater apenas a essa antena, iniciando-se pelo traçado geométrico da mesma.


2.COMO SE DETERMINA A CURVATURA DA SUPERFÍCIE DE UMA ANTENA PARABÓLICA SIMÉTRICA?

Apesar de parecer extenso este artigo, entendemos necessário descer o véu que naturalmente cerca um assunto técnico dessa natureza, de interesse quase sempre de robistas. Primeiramente, vamos conhecer a fórmula da qual deriva a geometria de nossa parabólica simétrica. A função f(x) = ax2+ bx + c é de uma parábola. Como não vamos descer a detalhes de formulações matemáticas - não é nosso objetivo, vamos passar para a forma reduzida da função f(x) que representa uma parábola e que nos interessa diretamente, ou seja:

f(x) = y = x2/4f

A animação abaixo, sem nos preocuparmos com graduação de escala no plano cartesiano, dá-nos uma idéia de como podemos traçar uma curva parabólica simétrica, a partir da função reduzida mencionada anteriormente. Nada tendo a ver com a plotagem simplesmente, já estamos nos adiantando e incluindo conceitos aplicáveis à antena parabólica, como distância focal, profundidade, diâmetro e relação foco/diâmetro.

3.PARABOLÓIDE DE REVOLUÇÃO E ANTENA PARABÓLICA SIMÉTRICA

Se, depois de plotarmos uma curva de uma parábola simétrica como na animação acima, fizermos com que essa curva gire em torno do eixo vertical y, a superfície assim gerada é denominada parabolóide. A construção de uma antena parabólica simétrica deriva da aplicação do parabolóide de revolução que possui um ponto focal localizado em algum lugar geométrico do eixo y. A figura abaixo mostra um parabolóide de revolução gerado da forma descrita anteriormente.

Fig. 02 - Parabolóide

4.CONCEITO DE PROFUNDIDADE APLICADO À ANTENA PARABÓLICA

Observamos que as formas construtivas das antenas parabólicas são diversificadas. Para um mesmo diâmetro, podemos ter antenas mais profundas e antenas menos profundas. As figuras abaixo, também de parabolóides de revolução, dão-nos idéia dessa variação de profundidade e, nessa consideração, vamos conceituar uma antena com rasa e outra como profunda. Vamos utilizar os parabolóides de revolução para exemplificar o conceito.

Fig. 03 - Superfície de uma antena profunda	Fig. 04 - Superfície de uma antena rasa

Queremos deixar claro que as figuras acima de parabolóides de revolução lembram antenas parabólicas, mas não são antenas parabólicas e as usamos para fins didáticos apenas.

5.ANTENA PARABÓLICA TIPO PONTO FOCAL E SUA ILUMINAÇÃO

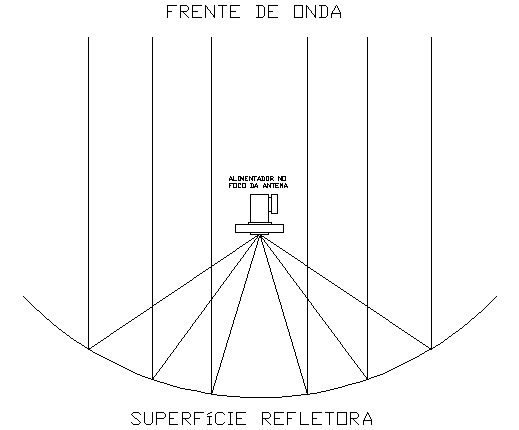
As antenas parabólicas simétricas derivadas do parabolóide de revolução exemplificado acima são construções que aproveitam as propriedades geométricas inerentes e a refletividade de sua superfície às ondas eletromagnéticas que chegam até ela, concentrando-as num único ponto denominado ponto focal, onde se coloca um elemento denominado iluminador, alimentador, que tem a função de recolher, de captar, o sinal dos satélites que caminham pelo espaço como ondas eletromagnéticas. A figura, a seguir, dá-nos uma visão de como se dá a reflexão dessas ondas, representadas por raios unitários que, depois de refletidos pela superfície parabólica, redirigem-se para o ponto denominado focal, onde está o iluminador, o alimentador.

Fig. 05 - Iluminação de uma superfície parabólica - ponto focal

6.EFICIÊNCIA DE ILUMINAÇÃO, PROFUNDIDADE E INTERFERÊNCIA TERRESTRE

Se a totalidade dos raios (estamos aqui representando as ondas eletromagnéticas por raios), depois de refletidos, atingissem e iluminassem ou alimentassem o elemento iluminador, o elemento alimentador colocado no ponto focal, diríamos que a eficiência de iluminação da antena seria de 100%. As antenas parabólicas de superfície telada têm, em média, uma iluminação de 55%, ou seja, sua eficiência de iluminação é adotada como sendo 0.55 . As antenas sólidas, de superfície fechada, têm uma eficiência de iluminação maior e pode chegar a 80%. A eficiência de iluminação vai depender do tipo de superfície refletora, da perfeição geométrica da conformação parabólica e da profundidade da antena, basicamente. Antenas mais rasas têm a possibilidade de melhor iluminar o iluminador ou alimentador, embora sejam mais susceptíveis às interferências terrestres, as frentes de ondas eletromagnéticas que atingem lateralmente a antena, cujas fontes são diversas e a mais representativas, os enlaces de microondas e outras transmissões afins. Antenas mais profundas têm a inconveniência de não iluminar satisfatoriamente o iluminador ou alimentador, nas antenas ponto focal, embora sejam menos susceptíveis às interferências terrestres, por oferecer às mesmas um certa barreira. As antenas profundas geralmente têm um sub-refletor colocado no ponto focal e o iluminador ou alimentador colocado abaixo desse sub-refletor. São as antenas tipo Cassegrain e as Gregorianas. Sua utilização é mais técnica, nas repetidoras, e transmissoras e não nas recepções domésticas de apenas TV (TVRO).

A PRÁTICA NA PRÁTICA

7.DADOS DO PROJETO DE UMA ANTENA PARABÓLICA PARA SE ENTENDER UMA PARABÓLICA

Nada melhor para se conhecer uma antena parabólica do que projetar uma telada simétrica e do tipo ponto focal. Vamos usar, nesse objetivo, o olho prático na escolha de alguns parâmetros.

Vamos considerar que se queira uma antena para receber satisfatoriamente um sinal de satélite irradiado numa localidade com a potência isotrópica efetiva de 40 dBw, polarizado no plano vertical (polarização linear) e banda C. Se consultarmos algumas Tabelas, vamos verificar que necessitamos de uma antena com um diâmetro de, aproximadamente, 2 metros. Então, já temos o diâmetro. Não se esqueça que falamos acima sobre a eficiência de iluminação de uma antena telada: 55%. Temos, então e também, a eficiência de iluminação da antena que é 0,55.
Poderíamos partir por outro caminho: verificar o ganho necessário da antena, para uma recepção satisfatória de 40 dBw de EIRP e, em função da frequência, da eficiência de iluminação e do ganho necessário, determinar o diâmetro. Mas, o diâmetro está escolhido: 2 metros. Falta escolher a relação f/D (foco/diâmetro) da antena.

Já verificamos que uma antena muita rasa fica vulnerável à interferência terrestre e uma antena profunda tem uma certa dificuldade técnica na sua iluminação. Assim, dentre as relações f/D usuais, vamos escolher, por exemplo, 0.36, ou seja f = 0.36 x D (foco = .72 m).

Voltando um pouco acima, verificamos a fórmula y = x2/4f. Essa será a fórmula a ser usada para o traçado da curva parabólica que servirá para conformar as nervuras da antena. Na fórmula, vamos variar x de 0 a 1 ( 1 é o raio da antena) e f (0.72m) será multiplicado por 4. Assim, teremos y = x2 dividido por 2.82 ou y = x2 / 2.82 .

De posse dessa fórmula, usando-se uma traçador ajudado por computador ou um papel milimetrado para um traçado manual, ter-se-á a curva gabarito para conformação das nervuras da antena. Então, é partir para o processo de fabricação da antena.

Já que a antena pode ser fabricada com os parâmetros escolhidos, qual seria a profundidade calculada dessa antena?

A profundidade da antena, como vimos, é medida do fundo da antena à sua borda diametral. Então, a profundidade é medida no ponto onde x assume o valor do raio que é 1, no nosso caso e, nessa consideração, o valor de y para x= 1 é o valor da profundidade, ou 35,5 cm.

Antena calculada, desenhada, construída, vamos passar diretamente ao local geométrico para onde deve convergir o sinal polarizado, ou seja o ponto focal da antena, onde vai estar o iluminador, o alimentador, acoplado ao seu LNB/LNBF e que necessitam de ajustes.


8.PARÂMETROS E PRÁTICAS DE AJUSTE DO ALIMENTADOR/ILUMINADOR

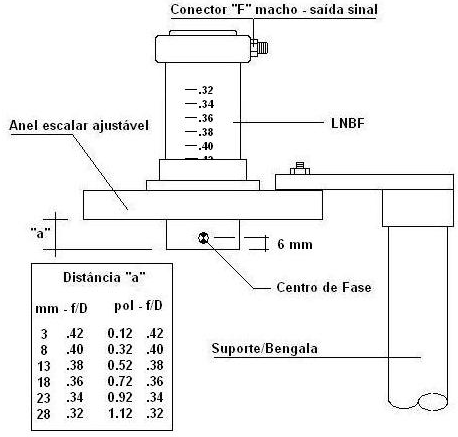
A figura que disponibilizamos, a seguir, procura evidenciar os parâmetros dimensionais para fixar e ajustar o conjunto iluminador no ponto focal, de forma correta e eficiente.

Fig. 06 - Ajustes entre disco escalar e guia de onda tubular LNB banda C

Na figura, vemos um conjunto LNBF (amplificador de baixo ruído integrado ao feeder (alimentador), inserido em um disco de anéis escalares. Geralmente, o corpo do iluminador, guia de ondas, vem com uma marcação que tem a finalidade de fixá-lo na posição correta, em relação ao disco escalar. Essa marcação pode variar de .32 a .42, adimensionais que representam relações f/D (distância focal dividida pelo diâmetro da antena).

O conjunto está fixo em um suporte no topo de uma haste, bengala, que pode sofrer giro. Observamos, ainda, uma marcação de um ponto virtual que seria o centro de fase do guia de onda, geralmente, para Banca C, localizado entre 6.0 e 6.5 mm (1/4") da boca do guia de ondas. Na figura, marcaram-se 6 mm. A distância entre esse centro de fase (virtual) e o fundo da antena (disco) deve ser numericamente igual à distância focal da antena. Nesse caso, a boca do guia ficará 6 mm abaixo do ponto focal que coincide com o centro de fase do guia de ondas. É importante, o centro de fase do guia fica sobre o foco da antena.

Uma outra distância a ser ajustada no conjunto é a que, na figura, está identificada como distância "a". Ela dependerá da relação f/D da antena. Na figura, há uma Tabela que dá a distância em mm e em polegadas. Selecione a distância, de acordo com a f/D da antena. No ajuste, ou se mede a distância a partir da boca do guia, ou se usa a marcação existente no corpo do guia - quando existir, para ajustá-la. Trave então o corpo do LNB/LNBF na posição devida. Esse ajuste está concluído.

Um final ajuste a ser feito é o do casamento da sonda vertical do LNB/LNBF com o plano de polarização do sinal sendo recebido. Vamos ver, então, como isso é feito.

9.AJUSTE E CASAMENTO DO PLANO DE POLARIZAÇÃO DO ILUMINADOR/ALIMENTADOR

Para que a máxima potência do sinal recebido do satélite seja transferida para o LNB/LNBF, através das sondas ortogonais de captação presentes no fundo do guia de ondas, torna-se necessário que as mesmas estejam no mesmo plano de polarização do sinal, melhor dizendo, no plano de propagação da componente elétrica do sinal. A figura logo abaixo esquematiza como o sinal de polarização linear se propaga pelo espaço, estando a componente elétrica do sinal em um plano vertical.

A Fig. 07 acima dá-nos uma aproximada idéia de como é visto o disco de anéis escalares, com o observador posicionado por debaixo da antena.

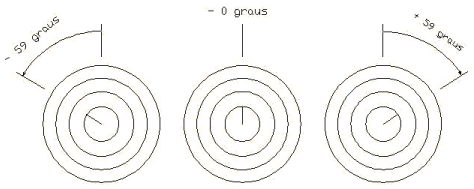
A Fig. 08 abaixo esquematiza a visão genérica que se tem da sonda vertical, com o ajuste do angulo de polarização em três distintas posições exemplificadas: menos 59 graus, zero graus e mais 59 graus.

Fig. 08 - Sonda vertical apontando três direções diferentes

O ajuste do ângulo de polarização pode ser feito de forma visual ou seguindo valores calculados. De forma visual, quando se gira a haste que suporta o conjunto iluminador ou, como se chama, a bengala. Gira-se a bengala até que se observe, na recepção, o máximo de sinal. Depois de verificar, em mais de um canal sintonizado, que a posição está correta, trava-se o giro da bengala (LNB banda C - Em banda Ku, gira-se o próprio LNBF).

A forma mais técnica é utilizar o valor do ângulo de polarização calculado e coincidir a direção da sonda vertical com esse ângulo. Nos programas de cálculo de direcionamento de antena numa determinada localidade, o ângulo de polarização para aquele satélite, naquela localidade, é sempre fornecido pelo programa.

Suponha-se que o ângulo seja menos 59 graus, ajusta-se a sonda como indicado na figura acima. Se for mais 59 graus, a posição é avançada 90 graus. Os satélites cuja posição orbital dada em longitude oeste (W) e que estão à esquerda do observador do hemisfério sul, olhando para o lado do equador terrestre, têm ângulo de polarização negativos.

Ao contrário, os que estão à direita do observador, têm ângulo de polarização positivos. Os satélites cuja posição longitudinal na órbita têm o mesmo valor da longitude do local da instalação têm o plano de polarização na vertical e o ângulo de polarização, nesse caso, é zero.


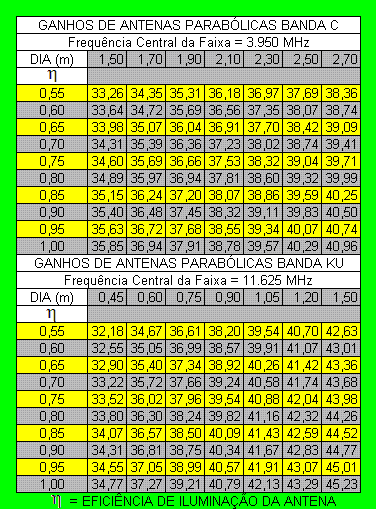
10.GANHOS DE ANTENAS PARABÓLICAS BANDA C E BANDA KU

O ganho de uma antena parabólica em relação a uma antena isotrópica pode ser determinado matematicamente, através do uso de fórmula em que o ganho se apresenta como função da frequência processada, do diâmetro da antena e da eficiência de iluminação (eta).

A frequência vai depender da faixa de recepção de interesse e, no cálculo do ganho, se utiliza uma frequência mediana da faixa.

O diâmetro será tanto maior quanto se necessite de um determinado ganho.

A eficiência de iluminação vai depender da forma construtiva, de sua conformidade com os traçados geométricos, da correção de sua superfície refletora e da maior ou menor facilidade em ser o conjunto focal iluminado pela frente de onda nele refletido, nele concentrado.

Na figura apresentada, podemos verificar como varia o ganho em função do diâmetro, em função da eficiência de iluminação (eta), considerando-se as frequências medianas das bandas especificadas.

A fórmula reduzida abaixo será utilizada para o cálculo do ganho de uma antena.

G = 10 x log [((3,14159 x d x f)2 x h) / 90000] onde:

G = ganho em relação a uma antena isotrópica, em dBi

d = diâmetro, em metro

h = eficiência de iluminação, variando de 55% a 100%

f = frequência mediana, em MHz.
Normalmente, se requer de uma antena um ganho mínimo de 37 dBi, para que a recepção ocorra de forma satisfatória, para EIRP mínimo de 38 dBw.
 

Fig. 09 - Quadro mostrando ganhos de antena